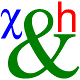
{ Practical astronomy | Optics and imaging | Telescopes and lenses }
Telescopes and lenses
Keplerian refractor
The design of the iconic astronomical telescope goes back to the early 17th century and to Kepler, who replaced Galileo's divergent eyepiece with a convergent one. Although a modern refractor will have a somewhat more complex lens assembly at the front, the principles of the optics are the same.
See the figure. Light from two stars (on the left, red and blue lightpaths, resp.) separated on the sky by an angle α enters the telescope through the large lens L at the front. The higher refractive index of the glass compared to the air, combined with the concave shape of the lens refract the parallel light rays so as to pass through a single point. For the star on the optical axis (red) this is the focal point; the small bright point is the image of the star. The second star (blue) forms an image some distance d away in the focal plane.
Keplerian telescope. The f/7 focal ratio is in fact more characteristic of a 21st century ED doublet achromat.
The characteristics of the telescope or any optics designed to image distant objects (think photo lens!) are captured by just two numbers. One is the aperture D, which is the diameter of the front lens L. The other is the focal length f, which is the distance between the lens L and the focal point F. This is true for astronomical refractors, photo lenses, but also astronomical reflectors.
Aperture and diffraction

Diffraction pattern of laser light after passing through a small aperture, with the Airy disc at the centre.
The aperture of a photo lens or telescope is simply the diameter of the front lens or primary mirror. It is usually assumed that the aperture is clear, even though in a mirror assembly the primary is partially obstructed by the secondary. The aperture is important for two properties of the optics.
First, if you double the aperture you quadruple the light-collecting area. A larger aperture collects more light from the object, giving brighter images, detecting fainter objects, permitting shorter exposures, permitting larger image scales, etc.
Second, if you double the aperture you halve the separation of objects that you can distinguish in the image. Image resolution is limited by quantum mechanics; in optics this effect is called diffraction.
One of the principles of quantum mechanics is Heisenberg's uncertainty principle. It states that one cannot simultaneously measure with arbitrarily high precision both the location and movement of a particle. In our case, the particle is a photon of light. We do not set out to measure the position of the photon, only its direction, i.e. where on the sky is the object that sent us the photon. However, we do restrict the photon's position as being within the aperture when it enters the telescope. This restricts the precision with which we can measure its direction of movement. The larger the aperture the smaller the spot on the sky to which we can pin down the source.
The number used to quantify the diffraction of a circular aperture is the apparent radius of the Airy disc (Airy 1835, Willingale 2012):
ΔαA ≈ 1.22 λ / D
where λ is the wavelength observed. The wavelength is usually set to that of green light, 550 nm. We should rewrite this so that you can insert your aperture in mm and read out the resolution in arc seconds ("):
ΔαA/" ≈ 140 mm / D
Hence, a 140 mm aperture can resolve two equally bright stars 1" apart. 70 mm can resolve such a double star only if the stars are 2" apart.
The Airy disc radius ΔαA is measured to the first minimum of the brightness pattern. Elsewhere, we will use this as approximation of the FWHM (full width at half maximum) or diameter at half the maximum brightness.
| D | ΔαA | optics |
|---|---|---|
| 1 mm | 113.0" | Panasonic Lumix DMC-TZ8, 1x, f = 4.1 mm, f/3.3 |
| 10 mm | 14.0" | Panasonic Lumix DMC-TZ8, 12x, f = 49 mm, f/4.9 |
| 10 mm | 14.0" | Sigma 55-200 mm, 55 mm, stopped down to f/5.6 |
| 25 mm | 5.6" | Sigma 55-200 mm, 200 mm, stopped down to f/8 |
| 63 mm | 2.2" | Telementor II achromatic doublet refractor |
| 80 mm | 1.8" | 80 mm, ED achromatic doublet refractor |
| 200 mm | 0.7" | 200 mm, Schmidt-Cassegrain reflector |
Focal length and image scale
Looking at the drawing of the Keplerian telescope, the focal length is what determines the scale of the image in the focal plane. Consider an angular radius or distance α from the optical axis on the sky; say the apparent radius of a planet or the separation of two components of a double star. A lens or telescope of focal length f projects this to a linear size d in the focal plane given by
d = f · tan α
Lens speed and f ratio
Consider observing or imaging an extended object, a planet, the Moon, a landscape to photograph. While a larger aperture collects more light, a larger focal length spreads this light over a larger image area. The two effects counteract each other, so that the ratio of focal length and aperture tells us how fast a lens or telescope is. The smaller f/D, the faster the lens and the brighter the image.
There is no clear rule how the term f ratio is used. It can be f/D, such as "my photo lens has an f ratio of 5.6". Or it can be D/f, such as "this is a 1/5.6 lens". Further, in photography, the term aperture is rarely used as linear diameter of the aperture, but as a synonym for the f ratio, such as "I used aperture f/5.6" or "I used aperture 5.6".
Eyepiece for visual observation
In order to look through a telescope one will put an eyepiece in the back. This acts similar to a magnifying glass to look at the image formed in the focal plane. Compared to looking at the sky with the naked eye, the telescope and eyepiece afford a magnification that is the ratio of the two focal lengths, telescope (index 1) and eyepiece (index 2).
M = f1 / f2
Sometimes the exit pupil is of interest. This is the size of the circle of light exiting the eyepiece. It is smaller than the aperture by a factor that is the inverse of the magnification.
D2 = D1 / M
The relevance of this lies in comparing it to the pupil of the astronomer looking through the telescope. If the eye pupil is smaller than the telescope's exit pupil then light is lost and the effective light collection of the telescope is less than D1.
From these considerations follow the smallest and largest useful magnification of a telescope. Assuming an eye pupil of 5 mm, the exit pupil should be D2 < 5 mm.
M > 0.2 · D1/mm
The highest sensible magnification has to do with the fact that excessive magnification will only make the limited resolution more noticeable. Assuming again 5 mm aperture for the naked eye, its resolution limit due to diffraction is about half an arc minute. The highest useful magnification is perhaps 5 times the ratio of the eye's resolution and the telescope's resolution. Plugging in the numbers:
M < D1/mm
For example, a telescope with 130 mm aperture has a useful magnification range of 26 < M < 130.
Prime focus
Just to avoid confusion, the simplest and cleanest way to use a telescope for imaging is to remove the eyepiece and the camera lens and place the camera's detector into the focal plane of the telescope. This is called using the prime focus.
Afocal projection
To the visual observer, afocal projection is a very intuitive way of combining a camera with a telescope. You insert an eyepiece E into the telescope and focus visually on the image at F1 by looking through the telescope. You focus the camera with its lens C for infinity, just as you relax your eye when focus sing the telescope. Hold the camera behind the eyepiece to replace your eye, and you can take a picture.
How bright will the image be and how large will the object be in the image? To answer this you need to calculate the aperture and focal length of the combined optics, telescope and eyepiece and camera lens. Fortunately, that is simple. The aperture is that of the telescope (so long as the camera pupil exceeds the telescope exit pupil). The focal length is that of the camera f3 multiplied by the magnification of the telescope.
D = D1
f = f3 · f1 / f2
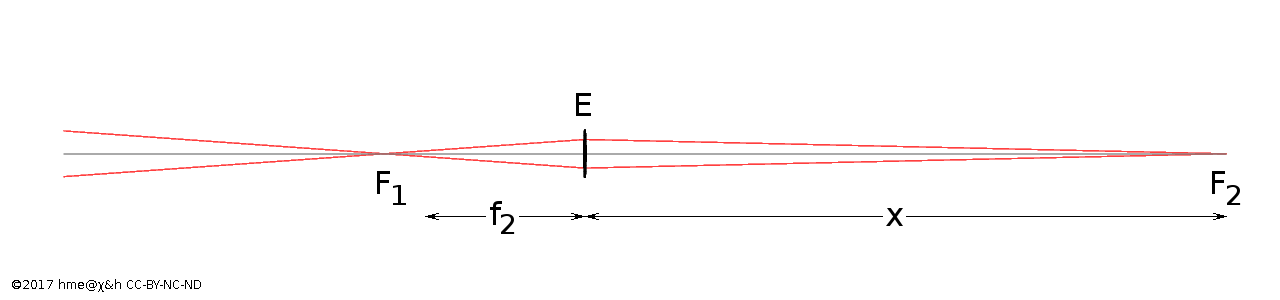
Eyepiece projection
In eyepiece projection, compared to afocal projection, we retain the eyepiece E but dispense with the camera lens. The eyepiece then re-projects the image created by the telescope at F1 onto the camera detector at F2. The first image has to be further than f2 in front of the eyepiece, and the second image will be a distance x > 2·f2 behind the eyepiece. In a special case, the distances are 2·f2 on either side and the second image has the same scale as the first. One might use this trick to move the image further outside the back of the telescope by a distance of 4·f2.
More likely, eyepiece projection is used to make a second image larger than the first. This would be because the telescope itself does not have sufficient focal length. If the distance to the camera is x then the combined focal length of telescope and eyepiece is
f = f1 · [(x/f2) − 1]
D = D1
There are a few practical difficulties that make the maths here all but meaningless. In particular, an eyepiece is not a thin lens and it is hard to know where from to measure the focal length or the separation x. You will have to find the best arrangement by trial and error. It is good to know, at least, that a shorter eyepiece and a larger distance to the camera each increase the image scale. Also, moving the camera back one eyepiece focal length increases the magnification by 1.
You will normally use a high magnification eyepiece. With an eyepiece for moderate magnification (longer f2) the optical assembly becomes unmanageably long. With a similar value of x and longer eyepiece focal length, you will find that eyepiece projection reduces the focal length rather than increase it.
Eyepiece projection is often not a good idea. For one, the eyepiece is not designed for this application; the second image will be distorted. Second, eyepieces have dusty surfaces close to the first image plane and project this onto the camera detector only slightly out of focus.
Aberration
All optical designs are inherently flawed, even if manufactured perfectly. These flaws need to be kept to a minimum or at tolerable levels. The worst flaw in a refracting telescope is that of chromatic aberration: Light of longer wavelength is refracted less than shorter wavelengths so that blue light has a shorter focal length than red light; this is called dispersion. Reflecting telescope do not suffer chromatic aberration, because reflection works the same for all wavelengths.
Another flaw stems from the spherical shape of the lens surfaces and is called spherical aberration: Light that passes near the centre of the lens has a longer focal length than light that passes near the periphery. This problem can be avoided with aspherical lenses, but these are more difficult and expensive to make, and they then may show comatic aberration, meaning that off axis the image is not in good focus. In astronomy this is a problem with reflecting telescopes: The primary tends to be parabolic rather than spherical to avoid spherical aberration, but it is then subject to coma.
There is also the issue of field curvature. While a star in the centre of the field (on the optical axis) is focused in the focal point F, off-axis stars may come to focus slightly ahead of this position. Schmidt cameras famously require the photographic glass plates to be bent into focus during exposure, because the field curvature is very pronounced given the wide fields of view in these cameras.
Achromat and apochromat
To significantly reduce chromatic aberration achromatic doublet lenses were invented in the 18th century. They have been common since the early 19th century. The second, divergent lens is made of different glass with different refractive index. The combination will bring red and blue light to a common focus, but colours in between may still have a somewhat different focal length. More complex and expensive apochromatic lenses improve this further and bring all visible light almost to the same focus.
Chromatic aberration is more noticeable for short fast lenses with small f/D. Refractors for amateur astronomers until the late 20th century were invariably as slow as about f/15, but today it is quite possible to buy f/7 or f/5 refractors. Perhaps the main difference is the availability of ED doublets that use "extremely low dispersion" glass. Among the fast refractors on sale are achromats (which must be avoided except as guide scope or if they are traditional with long f ratio), cheap ED achromats (which should be avoided), moderately expensive ED achromats and very expensive apochromats. There are also so-called "apochromats" that are actually achromatic doublets, but hopefully of a quality similar to real apochromats. A good (pricey) ED doublet is often the best compromise between noticeable quality and affordability.
Field flattener
Spherical aberration is much reduced in achromats and apochromats. Field curvature can be reduced with an optical element near the back of the telescope. Current achromat or apochromat offerings to amateur astronomers may have such field flatteners as optional extras; these may also reduce the focal length, widen the field and make the f ratio faster. However, a field flattener will also create faint reflexes, leading to an inverted image of the very brightest stars superimposed on the original image.
Photo lenses

The Carl Zeiss museum in Jena displayed this Praktika SLR, demonstrating that a photo lens is not exactly "thin".
A photo lens can be an alternative to a telescope for astrophotography. In fact, telescopes have long focal length and only a small field of view. To image large areas of the sky you need to use a photo lens – mild tele, standard or wide-angle. While a Keplerian or traditional achromatic telescope are slower than f/10 or f/20, photographic cameras and film emulsions require much faster lenses. Photography is also not limited to landscapes at large distance, but includes architecture and portraits. And photographers want to control depth of field and require to control both the exposure time and the aperture. On the other hand, landscapes and portrayed persons are less exacting motifs for the lens than a field of bright pinprick stars on a totally black background.
Photo lenses then are much more complicated designs that make different compromises than telescopes. Refracting telescopes approach the ideal of a "thin lens", but a typical photo lens is very roughly as thick as its focal length is long.
In the range of focal length where you have the choice between a super tele lens for photography and a good ED doublet refractor, the latter probably gives superior image quality.
Finally, a telescope is designed to be used with its full, fixed aperture. A photo lens is designed to be used at its widest aperture only in exceptional circumstances; the image quality is far better if the aperture is reduced by one "stop" (by a factor √2), e.g. from f/4 to f/5.6.
Reflectors
While a refracting telescope is more straightforward in design, reflecting telescopes have some advantages. Reflection applies to all wavelengths of light equally and there is no chromatic aberration. The primary mirror is a single optical surface, whereas the Keplerian telescope lens has two surfaces and the light must traverse the block of glass that is the lens. Achromats have two lenses with four optical surfaces. A lens can be supported only at its periphery, while a mirror can be supported throughout its back surface.
James Gregory designed a reflecting telescope in 1663. This was similar to the later Cassegrain design, with a parabolic primary mirror, but an elliptical secondary instead of Cassegrain's hyperbolic secondary. By the time Robert Hooke built the first Gregory-design telescope in 1673, the designs by Newton and Cassegrain had entered the scene. Gregory later was professor at St Andrews University, which ironically has a Schmidt-Cassegrain telescope named after James Gregory (Cameron 2017). Following harsh criticism by Huygens, the identity of Cassegrain remained a mystery until 1997 (Baranne and Launay 1997).
Bernhard Schmidt, in 1931, invented the Schmidt camera, which has a spherical primary mirror and a transparent corrector plate at the front. The corrector has a complicated surface figure such that it preemptively corrects the direction of incoming light rays to eliminate the spherical aberration of the primary. In the mid 20th century a combination of the Schmidt design and the Cassegrain design was developed at Mount Wilson Observatory and at the University of St Andrews (Jack 1951). In the 1970s such a design became available to amateur astronomers as an affordable, compact telescope with large aperture and focal length.
Today, the two reflector designs most accessible to amateur astronomers are the Newtonian (including those on a Dobsonian mount) and the Schmidt-Cassegrain.
Newtonian

Newtonian telescope. The f/5 focal ratio is typical of small amateur telescopes on the market today.
Newton's design of a reflecting telescope is almost as simple as Kepler's design of a refracting telescope. Instead of a lens focusing the light that passes through, a primary mirror P at the back of the telescope tube focuses the light it reflects back to the front of the tube, where the image would be formed at the focal point F. The immediate problem is that the astronomer and her eyepiece cannot be brought in to look at the image, because they would obstruct the tube opening and stop any light from being received. Newton simply suspends a planar secondary mirror S near the front of the tube to divert the returning light at right angles to the side of the tube.
As with lenses, a spherical mirror is easier and cheaper to make, but exhibits the flaw of spherical aberration. Therefore, the primary is given a parabolic shape in order that all radial zones of the mirror have the same focal length and a common focal point F. However, this causes another flaw called coma. Consider the images of two stars in focus, one on the optical axis and the other on the periphery of the field of view. Whereas a spherical mirror would image both stars at identical quality due to the symmetry of the spherical shape, a parabolic mirror off axis does not concentrate all light from the star in a single point.
Another disadvantage compared to the refractor is the obstruction that the secondary mirror introduces. This degrades the diffraction pattern. Although the Airy disc is of the same size as for a refractor of the same aperture, the secondary rings around the Airy disc are brighter. This leads to a reduced contrast when working near the resolution limit of the telescope.
In practical terms, however, reflecting telescopes are superior to refractors. The performance to price ratio is better, and large telescopes for professional astronomers are simply not feasible as refractors. The largest refractors have apertures of about 0.7 m to 1 m and were built in the late 19th to early 20th century, except for the 93 cm Swedish Solar Telescope of 2001. Contrast this with the 4 m stiff-mirror telescopes of the mid 20th century and the 8 m flexible-mirror telescopes of the late 20th and early 21st century. Apertures of 30 m to 40 m are now being planned and built, which will have segmented mirrors.
For the amateur astronomer, a 130 mm parabolic f/5 Newtonian like shown in the drawing is a beginner instrument, whereas the 80 mm f/7 ED doublet shown as "Keplerian" is a wide-field instrument for the serious amateur.
Schmidt-Cassegrain
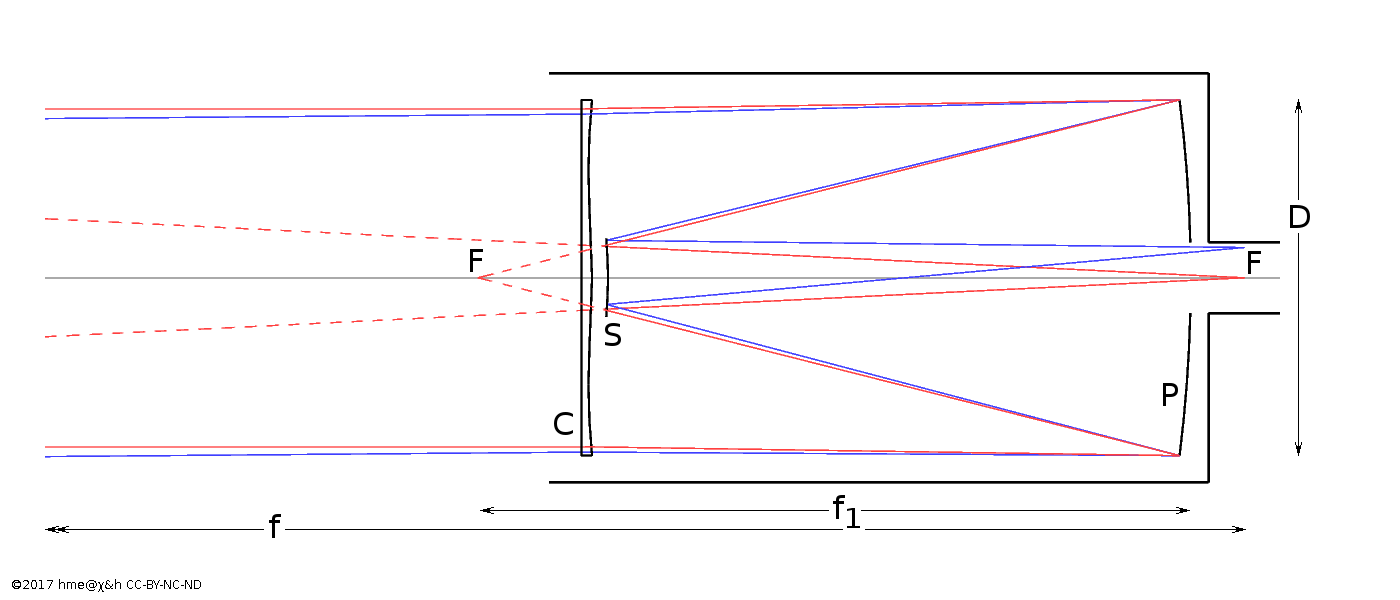
Schmidt-Cassegrain telescope. This is a typical design for a serious amateur telescope. The aperture is 200 mm, the primary is f/2 (400 mm focal length), the tube is about that length, but the overall focal length is 2000 mm.
The Schmidt-Cassegrain combines two designs of professional reflecting telescopes. The Schmidt camera was used for much of the 20th century for wide-field photography such as the Palomar survey of the northern sky and the survey of the southern sky conducted jointly by the European Southern Observatory from Chile and the United Kingdom from Australia. However, because the Schmidt design demands an aperture-sized sheet of glass with optically precise surfaces, at 1 m to 1.2 m the apertures of these instruments had reached their limit. Schmidt cameras are very fast at about f/3.3.
The Cassegrain design remains at the forefront of astronomical instrumentation. The 4- and 8-metre class telescopes built since the 1970s feature a large primary mirror P similar to the Newtonian. The secondary S sends the light back through a central hole in the primary to the Cassegrain focus F. Many of these large professional telescopes can be reconfigured to have an observer cabin at the primary focus, or to have a Newtonian tertiary mirror coincident with the altitude axis of the mount. The latter is called the Nasmyth focus after the Scottish engineer, artist and amateur astronomer James Nasmyth.
The Cassegrain secondary is not planar but hyperbolic, which acts to increase the focal length. This leads to a compact build, as the tube is as short as the primary focal length f1, while the image scale is as large as given by the overall focal length. In the drawing, notice the red rays extended from the Cassegrain focus through the secondary towards the sky. The combined focal length f reaches out to the point where these intersect the incident rays, far beyond the left edge of the drawing.
In the 1970s, Celestron began to market Schmidt-Cassegrain designs to amateur astronomers, with a choice of aperture of 5 in. (125 mm), 8 in. (200 mm) and 14 in. (355 mm). Today Celestron and Meade offer serious amateur telescopes of this design at a number of apertures between 8 in. and 16 in.
The build is even more compact than a Cassegrain or a Schmidt camera. A regular Cassegrain would have a moderately fast primary, but the Schmidt-Cassegrain inherits the fast Schmidt primary and drives this even further. A Schmidt camera would have the corrector plate at twice the primary focal length in front, while the Schmidt-Cassegrain moves the corrector near the primary focus, halving the tube length. The Schmidt-Cassegrain does not inherit the large field of view from the Schmidt camera. In comparison the Schmidt-Cassegrain image surface is almost flat.