Radioastronomisches Praktikum

Während den Amateurastronomen die optische Astronomie einfach als Fortführung ihrer eigenen Beobachtungstechniken mit besseren Mitteln erscheinen mag, dürfte die Radioastronomie wohl für viele ein Buch mit sieben Siegeln sein. Die Meßergebnisse der optischen Astronomie sind meist leicht begreifbar: Eine Fotoplatte zeichnet das Bild auf, das der Astronom sonst sehen würde; bei der Photometrie wird die Helligkeit gemessen, wobei evtl verschiedene Farbfilter zwischengeschaltet werden; ein optisches Spektrum schließlich ist uns allen halbwegs vertraut, und man kann mit einem Prisma alle Teile des Spektrums auf einmal fotografieren.

All dies ist bei der Radioastronomie nicht gegeben. A priori ist Radiostrahlung unserem Geiste völlig unbegreifbar, da wir keine Alltagserfahrung damit haben. Deshalb möchte ich hier einen Bericht geben von eine Radiobeboachtung, bei der ich als Teilnehmer an einem Praktikum zugesehen habe. Beobachtet wurde mit dem 25 m-Radioteleskop der Universität Bonn auf dem Stockert in der Eifel. Dabei wird zur Erklärung auch viel Theoretisches über Radiostrahlung und -teleskope zu sagen sein.

Für die Strahlungstheorie von großer Bedeutung ist die Schwarzkörperstrahlung. Ein ideal schwarzer Körper absorbiert alle Strahlung, die auf ihn fällt, während ein metallisch glänzender Körper alle Strahlung reflektiert. Dennoch gibt ein Schwarzer Körper Strahlung ab, die nur von seiner Temperatur abhängt (und nicht etwa von seiner chemischen Zusammensetzung). Interessant ist nun das Spektrum einer solchen Schwarzkörper-Strahlung, es wird wiedergegeben durch das Planck'sche Strahlungsgesetz. Für den langwelligen Teil (also etwa für den Radiobereich des elektromagnetischen Spektrums) kennt man seit langem eine Näherung, die die Flußdichte in Abhängigkeit von der Temperatur und Wellenlänge angibt. Es ist das Rayleigh-Jeans'sche Gesetz:

B_ν = 2 k T / λ²          (k = 1.3806 10^-23 W s / K)

Beobachten wir z.B. die Sonne mit einem H_α-Filter, so sind:

T = 5800 K (5527°C) die Temperatur
λ = 656.3 10^-9 m die Wellenlänge
B_ν = 3.72 10^-7 W / (m² Hz rad²)
B_ν = 1.13 10^-10 W / (m² Hz (°)²)

Dies bedeutet, daß 1 m² der Sonnenoberfläche in einem Frequenzband von 1 Hz (entspricht 1.44 10^-21 m Wellenlänge) und in jedes Quadratgrad seiner Himmelshalbkugel die Leistung von 1.13 10^-10 Watt strahlt. Diese Größe ist nun so schlau gewählt, daß ich die Deutung auch umdrehen kann: Wenn ich ein Teleskop von 1 m² Linsenfläche habe und damit ein Quadratgrad Sonnenoberfläche beobachte, und wenn schließlich mein H_α-Filter nur 1 Hz Bandbreite durchläßt, so erreicht mein Auge die Leistung von 1.13 10^-10 Watt.

Nun hat mein Teleskop aber nur 0.0314 m² Lichtsammelfläche. Außerdem ist das Gesichtsfeld nur 10' im Durchmesser, hat also 0.0218 (°)². Dafür ist die Bandbreite eines H_α-Filters mindestens 10^-10 m, entsprechend 6.94 10¹⁰ Hz. Mit diesen Werten steigt die Gesamtleistung auf 5.4 Milliwatt!! (Diese Leistungen sind etwa um einen Faktor 11 zu hoch, da B_ν nach genauer Rechnung mit dem Planck-Gesetz 3.28 10^-8 W / (m² Hz rad²) ist. Der Fehler ist so groß, weil die H_α-Linie relativ nahe beim Maximum der Planck-Kurve (Abb.1) ist. Für die Radioastronomie reicht die Rayleigh-Jeans-Näherung völlig.)

Ein großer Teil der kosmischen Strahlung ist tatsächlich Schwarzkörper-Strahlung. Wenn die Radioastronomen eine Strahlungsleistung vom Himmel messen, so können sie daraus nach dem Rayleigh-Jeans-Gesetz eine Temperatur ausrechnen. Diese muß allerdings nicht die echte Temperatur der Strahlungsquelle sein. Man beachte, daß die so berechnete "Temperatur" proportional zu B ist!

In wie weit kann man obige Betrachtungen zur optischen Beobachtung auf die Radioastronomie übertragen? Für den Amateurastronomen ist die Beobachtung mit einem Filter außergewöhnlich. Ein Radioteleskop mißt hingegen bei einer bestimmten Wellenlänge, wie oben angenommen. Wir haben oben weiter vernachlässigt, daß wir im Gesichtsfeld Einzelheiten wie Sonnenflecken beobachten können. Gerade dies wäre in der Radioastronomie nicht möglich, ein Radioteleskop kann tatsächlich nur die Gesamtstrahlung aus seinem "Gesichtsfeld" messen und keine kleineren Einzelheiten erkennen. Daher ist obige Betrachtung voll übertragbar: Wir haben einen Teleskopspiegel als Strahlungs-Sammelfläche und einen Empfänger mit bestimmter Empfangsfrequenz und bestimmter Bandbreite. Doch wie steht es mit dem Gesichtsfeld?

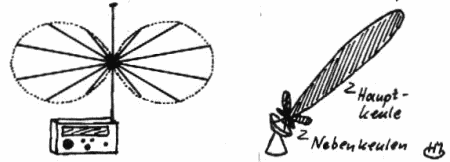
Dazu müssen wir die Empfangscharakteristik einer Radioantenne betrachten, die von ihrer geometrischen Gestalt abhängt. Wir alle kennen die Teleskopantenne am Kofferradio. Steht die Antenne senkrecht, so ist der Empfang aus allen Richtungen (in der Horizontebene) gleich gut. Steht die Antenne jedoch waagerecht, so beobachten wir eine Richtwirkung: Für optimalen Empfang steht die Antenne senkrecht zur Empfangsrichtung.

Diese Eigenschaften einer Antenne drückt man durch ihre Charakteristik aus: Je weiter in eine Richtung die "Keule" reicht, desto besser ist der Empfang aus dieser Richtung. Die Charakteristik eines Radioteleskops hat eine Hauptkeule in deren Richtung der Empfang optimal ist. Jedoch hat diese Hauptkeule eine endliche Winkelausdehnung, und diese können wir als "Gesichtsfeld" betrachten. Die gemessene Leistung kommt also im Wesentlichen aus der Richtung der Hauptkeule, einem endlich großen Bereich am Himmel.

Es ist jedoch noch anzumerken, dass die Nebenkeulen auch eine Rolle spielen. Durch sie wird - wenn auch stark gedämpft - eine Störstrahlung empfangen, z.B. von einem benachbarten Wald. Diese sogenannte Bodenstrahlung ist von Natur aus sehr stark (im Vergleich zum Kosmos ist die Erde eben ziemlich heiß) und macht sich trotz der Dämpfung noch bemerkbar.

Doch nun zum Radioteleskop Stockert. Über den Hauptspiegel von 25 m Durchmesser und den Sekundärspiegel kommt die Strahlung in das Empfangshorn. Ein Hohlleiter führt die Strahlung zum Empfangsverstärker. Nach einer weiteren Verstärkung des Signals wird durch Filter und Mischer die gewünschte Empfangsfrequenz ausgewählt. Dieses Ausgangssignal wird dann digital gemessen und von einem Computer auf dem Bildschirm in regelmäßigen Abständen geschrieben. Zur Auswertung kann dieses digitale Signal auf Magnetband geschrieben werden, zusammen mit Zeit, Sternzeit, Rektaszension, Deklination usw. Im Teleskopspiegel ist neben dem Empfangshorn ein kleines Sendehorn angebracht, das in regelmäßigen Abständen von 16 msec ein bekanntes Signal sendet. Dieses Signal wird natürlich vom Empfangshorn auch empfangen und dient zur Eichung der digitalen Leistungsanzeige. Dies ist wichtig, denn die Leistungsanzeige vom Computer erfolgt nicht in Watt oder einer bekannten Einheit, sondern in einer zufälligen, unbekannten aber konstanten Einheit.

Wir hatten oben gesehen, daß aus der gemessenen Leistung die "Temperatur" bestimmt werden soll, die der Leistung proportional ist. Die gemessene Leistung setzt sich nun aus mehreren Komponenten zusammen:

1. Rauschen des Empfängers aufgrund dessen Temperatur (T_E)
2. Strahlung der Atmosphäre (Beitrag zu T_S)
3. Strahlung des Erdbodens (Beitrag zu T_S)
4. Strahlung des Himmels (kosm. Strahlung, T_A)
5. Strahlung des Eich-Horns (T_R)

Die vom Computer angezeigte Leistung ist die Summe der fünf Einzelleistungen und daher ist die entsprechende "Temperatur":

T_E + T_S + T_A     bzw.     T_E + T_S + T_A + T_R

Nun ist es möglich, statt der Antenne einen ganz gewöhnlichen elektrischen Widerstand vor den Empfänger zu schalten. Dann werden T_S, T_A und T_R ersetzt durch die physikalische (echte) Tempearture des Widerstandes, also 298 K entsprechend 24.8°C, und die "Temperatur" wird T_E + 298 K.

Zur Eichung richten wir nun das Teleskop zum Polarstern. Von dort erreicht uns so gut wie keine kosmische Strahlung. Der Computer zeigt:

P(T_E+T_S) = 2140          P(T_E+T_S+T_R) = 2400

Wird die Antenne durch besagten Widerstand ersetzt, so lautet die Anzeige:

P(T_E+298K) = 7400

Schließlich hat die Erfahrung gezeigt, daß die Atmosphären- und Bodenstrahlung zusammen etwa T_S = 12 K ausmacht. Die kosmische Strahlung war ja vernachlässigbar. Wir erhalten:

P(1K) = (1/286) [P(T_E+298K) - P(T_E+T_S)]
P(1K) = P(286K) / 286
P(1K) = 18.39
T_E = P(T_E+T_S) / P(1K) = (2140/18.39 - 12) K
T_E = 104.36 K
T_R = [P(T_E+T_S+T_R) - P(T_E+T_S)] / P(1K)
T_R = (2400 - 2140) K / 18.39
T_R = 14.14 K

Einer "Temperatur" von 1 K entspricht also eine Computer-Anzeige von 18.39, das Empfänger-Rauschen beträgt 104.36 K und das Eichsignal 14.14 K. Bleibt anzumerken, daß die kosmische Strahlung, die uns interessiert, es selten auf 1 K bringt, also verschwindend klein gegenüber dem Empfängerrauschen ist.

Wir wollen nun versuchen, die Qualität des Teleskops zu beurteilen. Dabei orientieren wir uns natürlich an der Charakteristik. Die Hauptkeule soll möglichst schmal und spitz sein, die Nebenkeulen möglichst klein. Die Schnitte durch die Charakteristik veranschaulichen die Bedeutung des Antennenraumwinkels Ω_A und des Hauptkeulenwinkels Ω_HK. Die gekennzeichneten Flächen sollen dabei jeweils gleich sein. Je kleiner Ω_HK ist, desto spitzer ist die Hauptkeule. Ω_HK steht in Beziehung zur Halbwertsbreite HPBW der Hauptkeule:

Ω_HK ~ 1.3 HPBW²

Ω_A hingegen bezieht die Nebenkeulen mit ein. Je näher der Wert von Ω_A and den von Ω_HK kommt, desto stärker ist die Empfangscharakteristik auf die Hauptkeule konzentriert. Daher heißt

Ω_HK / Ω_A     die Hauptkeuleneffektivität.

Schließlich gilt für die effektive Antennenfläche

A_e = λ² / Ω_A          wo λ: beobachtete Wellenlänge

Diese Fläche ist kleiner als die physikalische Spiegelfläche, da in der Antenne Verluste auftreten.

Wie kommen wir nun zu den Antennentemperaturen (die wir bisher "Temperatur" nannten)? Die Antenne mißt ja nicht einen Punkt am Himmel, sondern immer gleich das ganze "Gesichtsfeld" Ω_A. Die gemessene Leistung ist:

P = B_ν Δν ΔΩ A_e          (Δν: Frequenzbandbreite)

ΔΩ ist die Winkelausdehnung des Gebietes am Himmel, aus dem wir die Strahlung empfangen: also Ω_A, falls die Quelle eine große Ausdehnung hat, oder die Winkelausdehnung der Quelle, falls sie klein ist. Aus der Beobachtung lassen sich diese beiden Fälle nicht unterscheiden.

Man nimmt nun einfach eine große Ausdehnung an und kann so ein B'_ν bestimmen (B'_ν ≠ B_ν, falls die Quelle klein ist):

P / A_e = B'_ν Δν Ω_A
P / A_e = (2 k T_A / λ²) Δν Ω_A
P / A_e = (2 k T_A / A_e) Δν
T_A = P / (Δν A_e) A_e / (2 k)          Antennentemperatur

A_e soll hier nicht gekürzt werden, weil P/A_e die Leistung pro Flächeneinheit ist, die von der Quelle kommt. Diese ist von der Größe des Teleskops unabhängig, Leistung und Antennentemperatur sind dagegen Teleskop-abhängig.

Tatsächlich wird B_ν für eine ausgedehnte Quelle nur über die Hauptkeule konstant sein (und in den Nebenkeulen Null):

P / A_e = B'_ν Δν Ω_HK
P / A_e = (2 k T_B / λ²) Δν Ω_HK

Daher ist die Teleskop-unabhängige Strahlungstemperatur für ausgedehnte Quellen:

T_B = (Ω_A / Ω_HK) T_A

Wir haben ja bereits herausgefunden, wie wir aus der Computeranlage am Stockert die Antennentemperatur T_A bekommen. Wenn wir nun noch für eine Radioquelle wissen, wie groß P/A_eΔν ist, können wir durch eine eigene Messung die effektive Antennenfläche des Stockert-Teleskops errechnen.

Der zweite Teil unserer Aktivitäten besteht in einer Messung der intensiven punktförmigen Radioquelle Taurus A. (Es handelt sich hierbei um den Pulsar im Crab-Nebel.) Wir lassen dabei die Punktquelle durch unsere Hauptkeule laufen, d.h. wir nutzen die tägliche Bewegung des Pulsars am Firmament. Kommt Tau A an den Rand der Hauptkeule, so wird zunächst ein schwaches Signal empfangen. Dieses wird stärker, bis Tau A mitten in der Hauptkeule sitzt. Danach wird das Signal wieder schwächer, weil die Empfindlichkeit des Teleskops am Rande der Hauptkeule wieder abnimmt. Die Abb.4 zeigt den zeitlichen Verlauf des Signals. Anschließend wurde das Eich-Horn eingeschaltet, um den Temperatur- und Zeitmaßstab zu liefern. (Die Computeranzeige wurde auf einen Y-t-Schreiber gegeben, dessen Schrieb Abb.4 zeigt.) Die Zeichnung ergibt

T_A = 56.7 K

Dies ist nicht als Temperatur des Pulsars zu deuten, weil (i) die Punktquelle als flächenhaftes Objekt angesehen wurde, (ii) die Pulsarstrahlung keine Schwarzkörper-Strahlung ist, sondern durch Elektronen im Magnetfeld entsteht, (iii) T_A abhängig ist vom Teleskop.

Aus der Literatur entnehmen wir, daß bei 11 cm Wellenlänge für Tau A:

P / (Δν A_e) = 740 10^-26 W / (m² Hz)

Mit dem k-Wert aus der ersten Gleichung ist:

A_e = 211.0 m²

Dies sind nur 43 % der physikalischen Antennenfläche. Mit λ = 0.11 m :

Ω_A = λ / A_e = 5.73 10^-5 rad² = 0.188(°)²

Der Antennenwinkel hat also einen Durchmesser von 30'. Wir können auch die Halbwertsbreite der Kurve bestimmen:

HPBW entpricht 1.36 min Rektaszension

Mit der Deklination von Tau A (22°) wird:

HPBW = 1.36 min (1° / 4 min) cos(22°)
HPBW = 0.315° = 0.005502 rad = 18.9'

Damit wird der Hauptkeulenwinkel:

Ω_HK = 1.3 HPBW² = 0.129(°)²

Dies entspricht einem Durchmesser von 24'. Und schließlich wird die Hauptkeuleneffektivität:

Ω_HK / Ω_A = 68.7 %

Eines der wichtigsten Resultate unserer Messung ist die Halbwertsbreite der Keule HPBW (= Half Power Beam Width). Sie repräsentiert das Auflösungsvermögen, das am Stockert bei 11 cm empfangener Wellenlänge also 18 Bogenminuten beträgt.

Ist die Strahlungsquelle weiter ausgedehnt als diese 18', so kann man mit einer Teleskopeinstellung nur einen Teil davon messen. Um die Quelle zu kartographieren, muß jeder Punkt der Karte am Himmel einzel gemessen werden. Da die Auflösung begrenzt ist, macht es keinen Sinn, die Meßpunkte beliebig dicht nebeneinander zu legen. Zu große Abstände bedeuten hingegen einen Verlust an Information über die Struktur der Strahlungsquelle. Optimal ist ein Punktabstand von 0.4 HPBW, bei und also 7.5'. Da die Radioquelle, die wir beobachten wollen, 2° Durchmesser hat, wählen wir als Größe der Karte 4° x 4° entsprechend 33 x 33 Meßpunkte.

Wir erwarten für unsere Quelle eine Strahlungstemperatur von

T_B ~ 0.2 K      also      T_A ~ 0.15 K

Als Gesamtstrahlung von Empfänger, Erdboden und Atmosphäre erwarten wir hingegen 115 K !! Unsere Aufgabe besteht also darin, in einem Signal von 115 K Veränderungen von 0.01 bis 0.02 K zu messen!! Je länger jeder Meßpunkt beobachtet wird, desto genauer ist dies möglich, und es zeigt sich, daß 1 Sekunde pro Meßpunkt ausreicht. Mit 1089 Meßpunkten ergibt das eine gesamte Beobachtungszeit von 20 Minuten.

Die Ausrichtung des Teleskops ist natürlich rechnergesteuert, und so gibt es auch ein Programm, das das automatische "Abtasten" einer Himmelsgegend möglich macht. Das Teleskop stoppt dabei nicht bei jedem Meßpunkg, sondern fährt gleichmäßig über das Meßfeld, wie Abb.5 andeutet.

Wie schon gesagt, ist das gemessene Signal ca 100 bis 1000mal stärker als die Strahlung der Quelle. Zudem ändert sich die Bodenstrahlung bei jedem der 33 Teleskop-Schwenks, da das Teleskop bei jedem Schwenk auch auf und ab schwenkt. Wir erkennen nun, warum wir das Meßfeld doppelt so groß wählten wie die Quelle. Die Umgebung der Quelle dient uns dazu, die Strahlung der Quelle von der restlichen Störstrahlung zu trennen. Dies ist nicht so einfach, wie Abb.6 andeutet. Störend können sich plötzliche Änderungen der atmosphärischen Strahlung sowie andere kosmische Quellen im Meßfeld auswirken.

Stellen wir nun aus den Meßdaten eine Karte zusammen, so werden wir erstaunt feststellen, daß sich viele waagerechte Strukturen zeigen. Diese entstehen durch unterschiedliche atmosphärische Bedingungen während verschiedener Scans. Daher empfiehlt es sich, das Meßfeld noch einmal abzutasten, diesmal aber in der anderen Richtung. Beide Überdeckungen werden dann zu einer gemeinsamen Karte verarbeitet, was ein ziemlich umfangreiches rechnerisches Unterfangen ist.

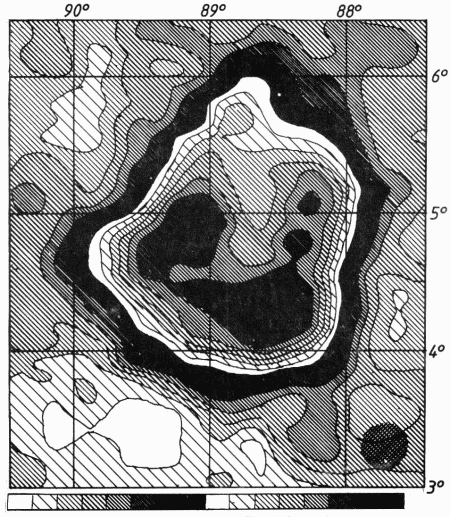
Doch schreiten wir zur Tat. Beobachtungsobject soll HB 21 sein, ein Supernova-Überrest bei der galaktischen Länge 89° und galaktischen Breite +4°, ca 5° nördlich Deneb im Sternbild Schwan. Nun hat man am Stockert natürlich nicht nur unser Objekt zu beobachten, vielmehr wird dort z.Z. der gesamte Himmel Stück für Stück gemessen und kartographiert. Messungen zu diesem Zweck sind an genaue Beobachtungszeiten bebunden; und so haben die Praktikumsteilnehmer noch zu warten, bis diese Messungen abgeschlossen sind.

Aber die Götter scheinen gegen uns verschworen; denn bevor es richtig losgehen kann, zieht ein Gewitter auf. Und ein nasses Empfangshorn eignet sich nicht für genaue Messungen. Und so warten wir darauf, daß sich das Wetter bessert. Man spricht schon davon, daß die Praktikumsteilnehmer nach Hause fahren können; ihre Tätigkeit würde sich ja ohnehin auf Zugucken beschränken. Doch schließlich reißen die Wolken auf, und um 22.17 MESZ kann es losgehen. Mit Spannung verfolgen wir den Schreiber, der uns die gemessene Leistung über der Zeit aufträgt, obwohl hier die Auflösung viel zu schlecht ist, um genaue Rückschlüsse auf die spätere Karte von HB 21 zu ziehen. Deutlich erkannten wir jedoch eine Punktquelle, die durch eine unbekannte kurzzeitige Störstrahlung verursacht wurde. Sie mußte später gesondert aus der Karte entfernt werden. Die erste Überdeckung (waagerecht, d.h. parallel zum galaktischen Äquator) ist um 23.36 abgeschlossen. Wir verzichten auf die Teilnahme an der zweiten Hälfte der Beobachtungen und fahren nach Bonn zurück.

Auf dem Stockert werden die Meßwerte gemeinsam mit Uhrzeit und Position am Himmel vom Computer auf Magnetband geschrieben. Im Radioastronomischen Institut der Universität Bonn werden die Daten vom Rechner dann verarbeitet. Zunächst besteht die Möglichkeit, "von Hand" einzelne Störungen aus der Karte zu eliminieren. Anschließend werden waagerechte und senkrechte Scans nach dem "Basketweaving"-Verfahren kombiniert. Dabei wird gleichzeitig die Neigung des Untergrundes, wie sie in Abb.6 veranschaulicht ist, abgezogen.

Die endgültige Radiokarte wurde aus insgesamt drei Überdeckungen berechenet, einer waagerechten und zwei senkrechten. Die Karte zeigt Linien gleicher Intensität im Abstand von 0.07 K Strahlungstemperatur. Die Skala der Grauwerte wird zweimal von weiß bis schwarz durchlaufen. Man erkennt die unvollständige Schalenstruktur. Der dunkle Kreis unten rechts bezeichnet die Größe der Halbwertsbreite.

Damit ist unser Ziel erricht, und mir bleibt, zu hoffen, daß ich Ihnen einen kleinen Einblick in radioastronomische Beobachtungspraxis geben konnte.

Horst Meyerdierks

---

TELESCOPIUM - Mitteilungen der Volkssternwarte Bonn Astronomische Vereinigung e.V.
Heft 40, Jahrgang 11 (1983), 2/1983
ISSN 0723-1121
Seiten 21, 23, 24, 25.